众所周知,无论我们的粒子加速器有多强大,粒子都永远不会被加速到光速或比光速还要快。例如,对于SLAC国家加速器实验室来说,主要的加速器是RF线性加速器,它可以加速电子和正电子直至50 GeV。具有该能量的电子的运动速度仅比光速慢2 cm / s。但是,显然,它仍然不能将粒子加速到光速。
为什么会这样呢?
对此,普遍接受的解释,是狭义相对论给出的解释。即:当粒子的速度增加到接近光速时,其质量(动量/能量)将急剧增加。如以下两个方程所述:
It is known to all that particles can never be accelerated to the speed of light or to be faster than the speed of light no matter how powerful our particle accelerators are built. For example, for the SLAC National Accelerator Laboratory, the main accelerator was anRF linear acceleratorthat acceleratedelectronsandpositronsup to 50GeV. This energy corresponds to the electron traveling at a speed within 2 cm/s of the speed of light. But still, it cannot accelerate particles to the speed of light.
Why?
The commonly accepted explanation to this is the explanation given by special relativity. That is, when the speeds of particles increase to near to the speed of light, its mass(momentum/energy) will increase dramatically according to special relativity. As described by these 2 equations:
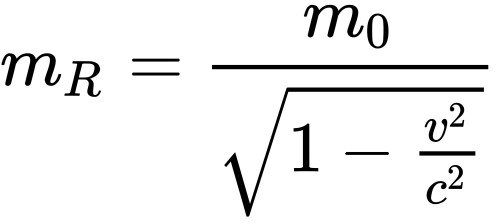
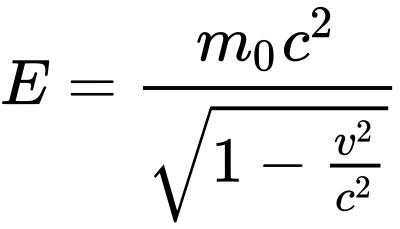
因此,尽管施加在粒子上的加速力不变,但是加速度已经变得小得多。结果是:粒子的速度越接近光速,加速度就越小。因此,粒子将永远无法达到光速。更不用说超过光速了。
这是一个合理的解释。但是,还有另一种合理的解释。也就是说,因为电场的运动速度等于光速,所以通过电场加速的粒子只能在光速范围之内进行加速,而永远无法达到光速。这意味着,当粒子速度增加时,施加在其上的力电场将变小。假设来说,如果粒子以光速运动,则其速度与电场的速度相同,那么,电场将不会对其造成加速。这类似于河中的石头或风中的沙子。如果河水推动石头移动,石头的移动速度永远不会比河水快。如果风推动沙子移动,则沙子的运动速度不会超过风速。如果这个解释正确,那么下面这两个方程将是错误的(并且狭义相对论的整个系统将是错误的):
Thus, although the accelerating force exerted on the particle is still the same, the acceleration become much smaller. The result is: the closer the speed of particles approaching light speed, the smaller the acceleration. So the particles will never reach the speed of light. Let alone exceeding the speed of light.
This is a reasonable explanation. But there can be another reasonable explanation. That is, because the speed of electric field is the speed of light, the particles accelerated by electric field can only be accelerated near the speed of light but can never reach the speed of light. This means, when the speeds of particles increase, the force electric field exerted on it will be smaller. For example, if a particle travels at the speed of light, it’s the same speed as the speed of electric field, then the electric field will not be an accelerating force to it. It’s similar to the stone in the river or sand in the wind. If the river water push a stone to move, the stone can never move faster than the river water. If the wind push sands to move, the sand will not move faster than the speed of the wind.
If this explanation is correct, the 2 equations will be incorrect(And the whole system of special relativity will be mistaken):
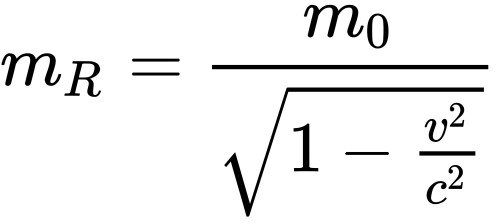
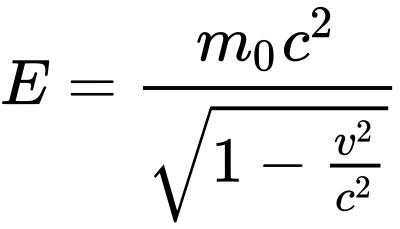
因为这两个方程都假定电场对快速移动的粒子施加的力是不变的,不论粒子移动的速度如何。根据相对论,这也是有道理的。但,这事实上可能是错误的。
在我的上一篇文章中,我已经证明了由狭义相对论推导的时间膨胀效应(钟慢效应)是不正确的。现在,如果上述两个方程式也被证明是不正确的,则狭义相对论显然是系统地错误的。
所以,现在我们有两个解释:
A,根据狭义相对论,当粒子的速度增加到接近光速时,施加在粒子上的电场力保持不变,但是粒子的质量(动量/能量)会急剧增加。当粒子的速度接近光速时,粒子的质量(动量/能量)几乎是无限的。
B,粒子的速度显然不能被加速到等于或者大于使粒子加速的电场的移动速度。当粒子的速度增加到接近光速时,其质量保持不变,但是施加在粒子上的电场力急剧下降。当粒子的速度几乎为光速时,电场施加在粒子上的力几乎为零。
Because both of these 2 equations assume that the force exerted by electric field upon fast-moving particles are the same no matter how fast the particles travel. This also make sense according to theory of relativity. But it can be wrong.
In my previous article, I already proved that the time dilation effect deduced from special relativity is incorrect. Now if the above 2 equations are proved to be incorrect, then the special relativity are apparently mistaken systematically.
So for these 2 explanations:
● A, according to special relativity, when the speeds of particles increase to be near the speed of light, the force electric field exerts on the particles remain the same, but the mass(momentum/energy) of particles will increase dramatically. When the speed of particles are almost speed of light, the mass(momentum/energy) of particles is almost infinite.
● B, particles cannot be accelerated to be faster than the moving speed of electric field that accelerates the particles. When the speeds of particles increase to be near the speed of light, its mass remain the same, but the force electric field exerts on the particles decrease dramatically. When the speed of particles are almost speed of light, the force electric field exerts on the particles is almost zero.
我们如何证明A或B是正确的?或者,理论上来说,A和B都有可能部分正确?
这里,本文发明一种实际的实验方法,可以用来得出结论。
实验设计如下:
我们首先将电子加速到非常接近光速的速度。例如,我们将其加速到光速的99.99999%。
此时,如果A是正确的,则该电子的质量(动量/能量)将非常大。如果B是正确的,则电场施加在粒子上的加速力将非常小。
无论如何,我们都让这个高速电子再通过一个M伏的加速电场,以进一步将电子加速到更高的速度,例如光速的99.9999999%。现在,我们仍然不知道A是正确的还是B是正确的。
How can we prove whether A or B is correct? Or theoretically, both A and B are partially correct?
There is a practical way to prove it.
A experiment can be designed as follows:
We first accelerate an electron to a speed very close to the speed of light. For example, we accelerate it to 99.99999% speed of light.
At this time, if A is correct, then the mass(momentum/energy) of this electron is very big. if B is correct, then the accelerating force electric field exerts on the particles is very small.
Either way, we send the electron through a M volts accelerating electric field to further accelerate the electron to a higher speed, for example 99.9999999% speed of light. Now we still don’t know whether A is correct or B is correct.
然后,我们让速度为光速99.9999999%的电子再次通过这个M伏的电场,但是这次,我们让电子以相反的方向通过。因此,这次,光速为99.9999999%的电子经历减速过程。
这样的话,如果A是正确的,则电子将以光速99.99999%的速度(或者至少将非常接近这个速度)从M伏的减速电场中出来。
但是,如果B是正确的,电子从M伏特电场中出来的时候,其速度将比99.99999%的光速低得多。这是因为,如果B 是正确的,则当电子从99.99999%光速提高到99.9999999%光速时,质量保持不变,但由于电子高速运动,导致其受到的加速力非常小。但是,当电子通过相同的M伏电场经历减速过程时,施加在粒子上的电场力,要比其经历加速过程时受到的电场力大得多。如果通过此实验,我们发现B是正确的,我们可以很容易地利用实验数据来总结一个公式,用来表达电场作用在电子上的力与电子运动速度之间的相互关系。
Then, we send the electron with 99.9999999% speed of light to the M volts electric field again, but for this time, we send it in the opposite direction. So for this time, the electron with the 99.9999999% speed of light will go through a decelerating process.
So if A is correct, the electron will come out of the M volts decelerating electric field with exactly the speed of 99.99999% speed of light. Or at least very near to it.
But if B is correct, the electron will come out of the M volts decelerating electric field with a speed much lower than 99.99999% speed of light. This is because when the electron increase speed from 99.99999% light speed to 99.9999999% light speed, the mass remain the same but the accelerating force is very small because of the high speed of the electron. But when the electron go through a decelerating process through the same M volts electric field, the force electric field exerts on the particles is much bigger than when it go through an accelerating process. If we find that B is correct, we can easily use the experiment data to summarize an equation explaining the relationship between the force electric field exerts on an electron and the speed of the electron.
如前所述,从理论上讲,亦有可能A和B都有部分正确。总之我们可以利用实验结果得出相应结论。
另外,如果B是正确的,我们现在将有一种方法可以将粒子加速到超光速:我们可以先在X轴方向上将粒子加速到接近光速。然后我们再在Y 轴方向上再次对它进行加速。这样,粒子的最终总速度将高于光速。
As said previously, it is also theoretically possible that both A and B are correct partially. Then we can also use the experiment results to arrive at a conclusion.
Additionally, if B is correct, we now have a way to accelerate particles to higher than speed of light: we can first accelerate the particles to near the speed of light. Then we accelerate it in a lateral direction. Then the final overall speed of the particles will be higher than the speed of light.
结论
● 关于加速器为何无法将粒子加速到光速的原因,可以有两种解释:
♦ A,相对论给出的解释。当粒子的速度增加时,施加在粒子上的电场力保持不变,但是粒子的质量(动量/能量)会增加。
♦ B,粒子的速度,显然不能被加速到等于或者大于使粒子加速的电场的移动速度。当粒子的速度增加时,施加在粒子上的电场力将减小,但粒子的质量保持不变。
● 从理论上讲,亦有可能A和B都是部分正确的。
● 本文发明了一个实际的实验方法,用来检验哪种解释正确。
● 如果解释B是正确的,那么相对论就是系统错误的。那么,将有一种简单的方法可以将粒子加速到超光速。
Conclusion:
· There can be 2 explanations as to why accelerators cannot accelerate particles to the speed of light:
o A, the explanation given by theory of relativity. when the speeds of particles increase, the force electric field exerts on the particles remain the same, but the mass(momentum/energy) of particles will increase.
o B, particles cannot be accelerated to be faster than the moving speed of electric field that accelerates the particles. when the speeds of particles increase, the force electric field exerts on the particles will decrease, but the mass of particles remain the same.
· It is also theoretically possible that both A and B are partially correct .
· A practical experiment is designed to examine the above explanations.
· If explanation B is correct, theory of relativity will be systematically mistaken, and there is a easy way to accelerate particles to speeds higher than the speed of light.